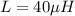Question

Tarik winds a small paper tube uniformly with 163 turns of thin wire to form a solenoid. The tube's diameter is 6.13 mm and its length is 2.49 cm . What is the inductance, in microhenrys, of Tarik's solenoid?

Answer 1

The inductance is
`L = 40\mu H`

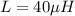
Step-by-step explanation:

From the question we are told that

The number of turns is
`N = 163 \ turns`

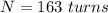
The diameter is
`D = 6.13 \ mm = 6.13 *10^(-3) \ m`

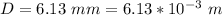
The length is
`l = 2.49 \ cm = 0.0249 \ m`

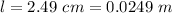
The radius is evaluated as
`r = (d)/(2)`

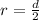
substituting values

`r = (6.13 *10^(-3))/(2)`

`r = 3.065 *10^(-3) \ m`

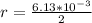
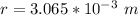
The inductance of the Tarik's solenoid is mathematically represented as

`L = (\mu_o * N^2 * A )/(l )`

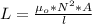
Here
`\mu_o` is the permeability of free space with value

`\mu_o = 4\pi *10^(-7) \ N/A^2`

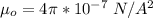
A is the area which is mathematically evaluated as

`A = \pi r^2`

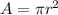
substituting values

`A = 3.142 * [ 3.065*10^(-3)]^2`

`A = 2.952*10^(-5) \ m^2`

substituting values into formula for L

`L = ( 4\pi *10^(-7) * [163]^2 * 2.952*10^(-5) )/(0.0249 )`

`L = 40\mu H`