Question

HELP PLEASE


find the domain of f and write your answer in interval notation​

Answer 1

(-infinity, 9/8]

Step-by-step explanation:

Domain is defined as all the possible x-values of a function.

`f(x) = 7√(9-8x) +4`

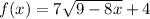
Lets test some negative numbers.

`f(-5) = 7√(9-8(-5)) +4 => 7√(49) +4 => a real solution`
`f(-1) = 7√(9-8(-1)) +4 => 7√(17) +4 => a real solution`

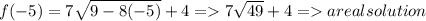
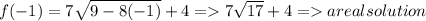
OK! That means all negative numbers should work!

What about 0?

`f(0) = 7√(9-8(0)) +4 => 7√(9) +4 => a real solution`

0 works..

Now, onto positive numbers?

`f(1) = 7√(9-8(1)) +4 => 7√(1) +4 => a real solution`

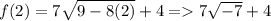`f(2) = 7√(9-8(2)) +4 => 7√(-7) +4` => imaginary

Check the last value that works. It can only be 9/8 because that's where the square root becomes 0, which is the last value before you head into the imaginary numbers..

`f(9/8) = 7√(9-8(9/8)) +4 => 7√(0) +4=>4`

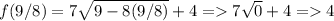
(-infinity, 9/8]