Question

The current particulate standard for diesel car emission is .6g/mi. It is hoped that a new engine design has reduced the emissions to a level below this standard. Set up the appropriate null and alternative hypotheses for confirming that the new engine has a mean emission level below the current standard. Discuss the practical consequences of making a Type I and a Type II error. (continue #5) A sample of 64 engines tested yields a mean emission level of = .5 g/mi. Assume that σ = .4. Find the p-value of the test. Do you think that H0 should be rejected? Explain. To what type of error are you now subject?

Answer 1

Explanation:

From the summary of the given statistics;

The null and the alternative hypothesis for confirming that the new engine has a mean emission level below the current standard can be computed as follows:

Null hypothesis:

`H_0: \mu = 0.60`

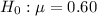
Alternative hypothesis:

`H_a: \mu < 0.60`

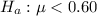
Type I error: Here, the null hypothesis which is the new engine has a mean level equal to .6g/ml is rejected when it is true.

Type II error: Here, the alternative hypothesis which is the new engine has a mean level less than.6g/ml is rejected when it is true.

Similarly;

From , A sample of 64 engines tested yields a mean emission level of = .5 g/mi. Assume that σ = .4.

Sample size n = 64

sample mean
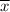`\overline x` = .5 g/ml

standard deviation σ = .4

From above, the normal standard test statistics can be determined by using the formula:

`z = (\bar x- \mu)/((\sigma)/(√(n)))`

`z = (0.5- 0.6)/((0.4)/(√(64)))`

`z = (-0.1)/((0.4)/(8))`

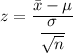
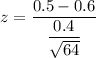
z = -2.00

The p-value = P(Z ≤ -2.00)

From the normal z distribution table

P -value = 0.0228

Decision Rule: At level of significance ∝ = 0.05, If P value is less than or equal to level of significance ∝ , we reject the null hypothesis.

Conclusion: SInce the p-value is less than the level of significance , we reject the null hypothesis. Therefore, we can conclude that there is enough evidence that a new engine design has reduced the emissions to a level below this standard.