Question

The structure of a house is such that it loses heat ata rate of 3800 kJ/h per8C difference between the indoors andoutdoors. A heat pump that requires a power input of 4 kWis used to maintain this house at 248C. Determine the lowestoutdoor temperature for which the heat pump can meet theheating requirements of this house.

Answer 1

The lowest outdoor temperature for which the heat pump can meet the requirement of the house is -9.6°C

Step-by-step explanation:

The coefficient of performance of a heat pump, COP, is given by the relation;

`COP_(hp) = (T_2)/(T_2 - T_1) = (Q_1* (T_2 - T_1))/(\Sigma W)`

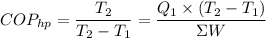
The rate of heat loss
`\dot Q_1` = 3800 kJ/h = 3800 ×1/60 × 1/60 kJ/s = 1.06 kJ/s

The power input = 4 kW = 4 kJ/s

The temperature indoors = 24 + 273.15 = 297.15 K

Therefore, we have;

`COP_(hp) = (297.15)/(297.15- T_1) = (1.06 * (297.15- T_1))/(4)`

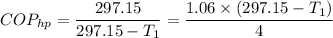
4×297.15= (297.15- T₁) × 1.06×(297.15- T₁)

Which gives;

18/19·T₁²-627.32·T₁+92014.97=0

(T₁ -263.59)·(T₁ - 330.71) = 0

The solutions are;

T₁ = 263.59 K or T₁ = 330.71 K

The lowest temperature = 263.59 K which is -9.6°C

The lowest temperature = -9.6°C.