Question

Determine the smallest distance x to a position where 450-nm light reflected from the top surface of the glass interferes constructively with light reflected from the silver coating on the bottom. The light changes phase when reflected at the silver coating.

Answer 1

Answer: B. The surface of the coating is rough, so light that shines on it gets scattered in many directions.

Explanation: On Edge!!!!!!!!!!!!!!!!!!!!

Answer 2

A wedge of glass of refractive index 1.64 has a silver coating on the bottom, as shown in the image attached below.

Determine the smallest distance x to a position where 450-nm light reflected from the top surface of the glass interferes constructively with light reflected from the silver coating on the bottom. The light changes phase when reflected at the silver coating.

Answer:

the smallest distance x = 2.74 × 10⁻³ m or 2.74 mm

Step-by-step explanation:

From the given information:

The net phase change is zero because both the light ray reflecting from the air-glass surface and silver plate undergo a phase change of
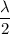`(\lambda)/(2)` , as such the condition for the constructive interference is:

nΔy = mλ

where;

n = refractive index

Δy = path length (inside the glass)

So, from the diagram;

`(y)/(x)=(10^(-5) \ m)/(0.2 \ m)`

`(y)/(x) = 5 * 10^(-5)`

`y = 5 * 10^(-5) x`

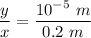
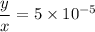
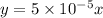
Now;

Δy can now be = 2 ( 5 × 10⁻⁵
`x`)

Δy =1 × 10⁻⁴
`x`

From nΔy = mλ

n( 1 × 10⁻⁴
`x` ) = mλ

`x = (m \lambda)/(n * 1 * 10^(-4) )`

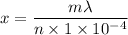
when the thickness is minimum then m = 1

Thus;

`x = (1 * 450 * 10^(-9) \ m)/(1.64 * 1 * 10^(-4) )`

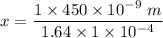
x = 0.00274 m

x = 2.74 × 10⁻³ m or 2.74 mm