Question

Question 1: Classify the system of equations and identify the number of solutions. 7x + 3y = 10 3y = 9 − 7x Answers: consistent, dependent; one inconsistent; one inconsistent; none consistent, dependent; infinite Question 2: Classify the system of equations and identify the number of solutions. 3x + y = 4 12x + 4y = 16 Answers: consistent, independent; one inconsistent; none consistent, dependent; one consistent, dependent; infinite Question 3: John and Harry went to a stationery shop. John bought 3 pens and 8 notebooks for $20.50. Harry bought 4 pens and 5 notebooks for $16.00. Identify the cost of a pen and the cost of a notebook. Answers: pen: $1.00; notebook: $2.50 pen: $2.00; notebook: $1.50 pen: $1.50; notebook: $2.00 pen: $2.00; notebook: $3.00

Answer 1

1. The equations is inconsistent and has no solution

2. The equations is consistent and has no solution

3. A pen costs $1.50 and a notebook costs $2.00

Explanation:

Solving
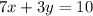`7x + 3y = 10` and
`3y = 9 - 7x`

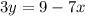
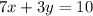`7x + 3y = 10` --- Equation 1

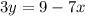`3y = 9 - 7x` --- Equation 2

Add 7x to both sides in equation 2

`7x + 3y = 9 - 7x + 7x`

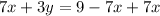
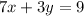`7x + 3y = 9` --- Equation 3

Subtract equation 3 from 1

`(7x + 3y = 10) - (7x + 3y = 9)`

`7x - 7x + 3y - 3y = 10 - 9`

`0 + 0 = 1`

`0 \\eq 1`

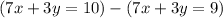
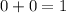
The equations is inconsistent and has no solution

Solving
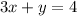`3x + y = 4` and
`12x + 4y = 16`

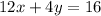
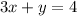`3x + y = 4` -- Equation 1

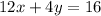`12x + 4y = 16` ---- Equation 2

Make y the subject of formula in equation 1

`y = 4 - 3x`

Substitute 4 - 3x for y in equation 2

`12x + 4(4 - 3x) = 16`

`12x + 16 - 12x = 16`

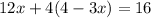
Collect Like Terms

`12x - 12x = 16 - 16`

`0 = 0`

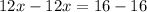
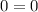
The equations is consistent and has no solution

3. Solving John and Harry

Given;

Represent Pen with P and Notes with N

John:
`3P + 8N = 20.5`

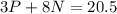
Harry:
`4P + 5N = 16.00`

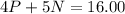
Required

Find P and N

Make P the subject of formula in equation 2

`4P = 16 - 5N`

`P = (16 - 5N)/(4)`

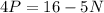
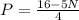
Substitute
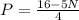`P = (16 - 5N)/(4)` in equation 1

`3P + 8N = 20.5`

`3((16 - 5N)/(4)) + 8N = 20.5`

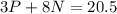
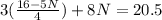
Open the bracket

`(48 - 15N)/(4) + 8N = 20.5`

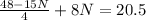
Take LCM

`(48 - 15N + 32N)/(4) = 20.5`

`(48 + 17N)/(4) = 20.5`

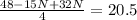
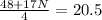
Multiply both sides by 4

`4 * (48 + 17N)/(4) = 20.5 * 4`

`48 + 17N = 82`

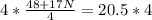
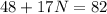
Subtract 48 from both sides

`48 - 48 + 17N = 82 - 48`

`17N = 82 - 48`

`17N = 34`

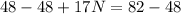
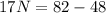
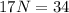
Divide both sides by 17

`17N/17 = 34/17`

`N = 34/17`

`N = 2`

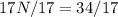
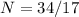
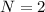
Substitute 2 for N in
`P = (16 - 5N)/(4)`

`P = (16 - 5 * 2)/(4)`

`P = (16 - 10)/(4)`

`P = (6)/(4)`

`P = 1.5`

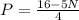
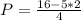
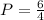
Hence, a pen costs $1.50 and a notebook costs $2.00