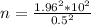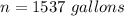Question

Trade associations, such as the United Dairy Farmers Association, frequently conduct surveys to identify characteristics of their membership. If this organization conducted a survey to estimate the annual per-capita consumption of milk and wanted to be 95% confident that the estimate was no more than 0.5 gallon away from the actual average, what sample size is needed

Answer 1

Complete Question

Trade associations, such as the United Dairy Farmers Association, frequently conduct surveys to identify characteristics of their membership. If this organization conducted a survey to estimate the annual per-capital consumption of milk and wanted to be 95% confident that the estimate was no more than 0.5 gallon away from the actual average, what sample size is needed? Past data have indicated that the standard deviation of consumption of approximately 10 gallons.

Answer:

The sample size is
`n = 1537 \ gallons`

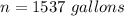
Explanation:

From the question we are told that

The margin of error is
`MOE = 0.5`

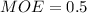
The confidence level is
`C = 95`%

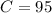Given that the confidence level is 95% the level of significance is mathematically represented as

`\alpha = 100 - 95`

`\alpha = 5`%

`\alpha = 0.05`

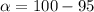
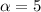Next we obtain the critical value of
`(\alpha )/(2)` from the normal distribution table , the values is
`Z_{(\alpha )/(2) } = 1. 96`

The reason we are obtaining critical values of

`(\alpha )/(2)`

instead of

`\alpha`

is because

`\alpha`

represents the area under the normal curve where the confidence level interval (

`1-\alpha`

) did not cover which include both the left and right tail while

`(\alpha )/(2)`

is just the area of one tail which what we required to calculate the sample size

Now the sample size is mathematically represented as

`n = \frac{[Z_{(\alpha )/(2) }] ^2 * \sigma ^2}{MOE^2}`

substituting values

`n = (1.96^2 * 10 ^2)/(0.5^2)`

`n = 1537 \ gallons`