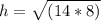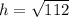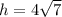Question

the altitude of the hypotenuse of a right triangle divides the hypotenuse into segments of lengths 14 and 8. what is the length of the altitude.

Answer 1

B.
`4√(7)`

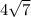
Explanation:

The right triangle altitude theorem states that the altitude of a right angled triangles formed on the hypotenuse is equal to the geometric mean of the 2 line segments it creates.

This can be represented as:

`h = √((xy))`

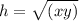
Where,

h = the length of the altitude,

x and y are the lengths of the 2 segments formed.

Therefore, the length of the altitude =
`h = √((14*8))`

`h = √(112)`

`h = √(16)*√(7)`

`h = 4√(7)`