Final answer:
To solve the inverse variation problem, we calculated the constant of variation using the given conditions and then applied it to find the new value of w when x=25, which is 1.6.
Step-by-step explanation:
To find the value of w when x is different from the original condition, we need to use the concept of inverse variation. In this case, w varies inversely as the square root of x. When x=4, w=4, we can write the inverse variation equation as:
w = k /
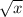
Where k is the constant of variation. To find k, we use the given values:
4 = k /
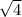→ k = 4 * 2 = 8
Now, to find w when x=25:
w = 8 /
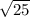= 8 / 5 = 1.6
Therefore, when x=25, w is 1.6.