Question

A certain group of women has a 0.86​% rate of​ red/green color blindness. If a woman is randomly​ selected, what is the probability that she does not have​ red/green color​ blindness?

Answer 1

The probability that a randomly selected woman has red/green color blindness is 0.9914

Explanation:

Given that the proportion of women having red/green color blindness is 0.86%

Represent that with p

`p= 0.86\%`

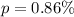
Convert proportion from percentage to decimal;

`p= (0.86)/(100)`

`p= 0.0086`

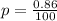
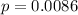
In probability; opposite probabilities add up to 1;

Let the probability that a woman selected have red/green color blindness be represented with q;

`p + q = 1`

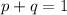
Subtract p from both sides

`p - p + q = 1 - p`

`q = 1 - p`

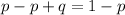
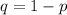
Substitute 0.0086 for p

`q = 1 - 0.0086`

`q = 0.9914`

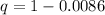
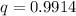
Hence, the probability that a randomly selected woman has red/green color blindness is 0.9914