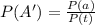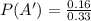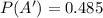Question

Factories A, B and C produce computers. Factory A produces 4 times as manycomputers as factory C, and factory B produces 7 times as many computers asfactory C. The probability that a computer produced by factory A is defective is0.04, the probability that a computer produced by factory B is defective is 0.02,and the probability that a computer produced by factory C is defective is 0.03. Acomputer is selected at random and found to be defective. What is the probabilityit came from factory A?

Answer 1

The probability is
`P(A') = 0.485`

Explanation:

Let assume that the number of computer produced by factory C is k = 1

So From the question we are told that

The number produced by factory A is 4k = 4

The number produced by factory B is 7k = 7

The probability of defective computers from A is
`P(A) = 0.04`

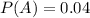
The probability of defective computers from B is
`P(B) = 0.02`

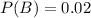
The probability of defective computers from C is
`P(C) = 0.03`

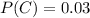
Now the probability of factory A producing a defective computer out of the 4 computers produced is

`P(a) = 4 * P(A)`

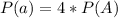
substituting values

`P(a) = 4 * 0.04`

`P(a) = 0.16`

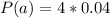
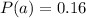
The probability of factory B producing a defective computer out of the 7 computers produced is

`P(b) = 7 * P(B)`

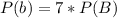
substituting values

`P(b) = 7 * 0.02`

`P(b) = 0.14`

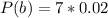
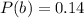
The probability of factory C producing a defective computer out of the 1 computer produced is

`P(c) = 1 * P(C)`

substituting values

`P(c) = 1 * 0.03`

`P(b) = 0.03`

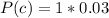
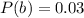
So the probability that the a computer produced from the three factory will be defective is

`P(t) = P(a) + P(b) + P(c)`

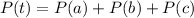
substituting values

`P(t) = 0.16 + 0.14 + 0.03`

`P(t) = 0.33`

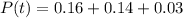
Now the probability that the defective computer is produced from factory A is

`P(A') = (P(a))/(P(t))`

`P(A') = ( 0.16)/(0.33)`

`P(A') = 0.485`