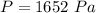Answer:
The pressure is
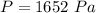
Step-by-step explanation:
From the question we are told that
The volume of the container is
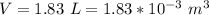
The mass of
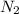 is
is
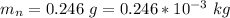
The root-mean-square velocity is
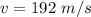
The root -mean square velocity is mathematically represented as
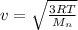
Now the ideal gas law is mathematically represented as
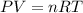
=>
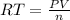
Where n is the number of moles which is mathematically represented as
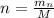
Where M is the molar mass of
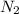
So
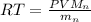
=>
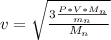
=>
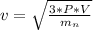
=>
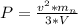
substituting values
=>
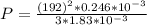
=>