Question

Heights of women (in inches) are approximately N(64.5,2.5) distributed. Compute the probability that the average height of 25 randomly selected women will be bigger than 66 inches.

Answer 1

the probability that the average height of 25 randomly selected women will be bigger than 66 inches is 0.0013

Explanation:

From the summary of the given statistical dataset

The mean and standard deviation for the sampling distribution of sample mean of 25 randomly selected women can be calculated as follows:

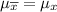`\mu_(\overline x) = \mu _x` = 64.5

`\sigma_(\overline x )= (\sigma)/(\sqrt n)`

`\sigma_(\overline x )= \frac{2.5}{\sqrt {25}}`

`\sigma_(\overline x )= (2.5)/(5)`

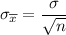
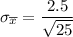
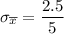
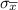`\sigma_(\overline x )` = 0.5

Thus X
`\sim` N (64.5,0.5)

Therefore, the probability that the average height of 25 randomly selected women will be bigger than 66 inches is:

`P(\overline X > 66) = P ( (\overline X - \mu_\overline x)/(\sigma \overline x )>(66 - 64.5)/(0.5) })`

`P(\overline X > 66) = P ( Z>(66 - 64.5)/(0.5) })`

`P(\overline X > 66) = P ( Z>(1.5)/(0.5) })`

`P(\overline X > 66) = P ( Z>3 })`

`P(\overline X > 66) = 1- P ( Z<3 })`

`P(\overline X > 66) = 1- 0.9987`

`P(\overline X > 66) =0.0013`

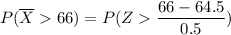
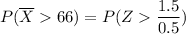
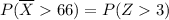
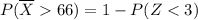
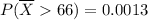
the probability that the average height of 25 randomly selected women will be bigger than 66 inches is 0.0013