Question

When Marilyn Monroe died, ex-husband Joe DiMaggio vowed to place fresh flowers on her grave every Sunday as long as he lived. The week after she died in 1962, a bunch of fresh flowers that the former baseball player thought appropriate for the star cost about $6. Based on actuarial tables, "Joltin' Joe" could expect to live for 25 years after the actress died. Assume that the EAR is 11.4 percent. Also, assume that the price of the flowers will increase at 3.3 percent per year, when expressed as an EAR. Assuming that each year has exactly 52 weeks, what is the present value of this commitment? Joe began purchasing flowers the week after Marilyn died.

Answer 1

Answer: $3,338.56.

Step-by-step explanation:

Given, EAR = 11.4 percent =0.114

Weekly interest rate=
`\frac{EAR}{\text{Number of weeks in a year}}=(0.114)/(52)=0.00219`

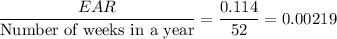
Growth rate of price of flowers = 3.3 % per year

Weekly growth rate=
`(0.033)/(52)=0.00063`

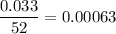
Star Cost (C)= $6

Time period (t)= 25 years

= 25 x 52 = 1300 weeks

Required formula for growing annuity :

`PV=(C)/(r-g)[1-((1+g)/(1+r))^t]`,

where C = Star cost

r = rate per period

g= growth rate

t = time period

`PV=(6)/(0.00219-0.00063)[1-((1+0.00063)/(1+0.00219))^(1300)]\\\\=(6)/(0.00156)[1-(0.998443408934)^(1300)]\\\\=(3846.15384615)[1-0.13197471131]\\\\=(3846.15384615)(0.86802528869)\approx\$3338.56`

Hence, the present value of this commitment = $3,338.56.