Question

In a game of rock-paper-scissors, you have a 1/3 chance of winning, a 1/3 chance of losing, and a 1/3 chance of tying in any given round. What is the probability that you will win at least twice in 3 rounds, given that there aren't any tied rounds in this particular match

Answer 1

In 3 rounds of rock-paper-scissors with no ties, the probability of winning at least twice is 0.5 when considering only wins and losses.

Step-by-step explanation:

Given that there are no ties in the particular match of rock-paper-scissors, we have a scenario with only two outcomes: win or lose. Since you have a 1/3 chance of each outcome in a three-round series with no ties, we adjust the probabilities to 1/2 for simplicity.

To calculate the probability of winning at least twice in 3 rounds, we can use the binomial theorem.

Let X be the number of wins. If there are no ties, the possible outcomes (number of wins) for X are 0, 1, 2, or 3. Since we need the probability of getting either 2 or 3 wins, we calculate these separately.

The formula for finding the probability of exactly k wins in n trials is P(X=k) = (n choose k) × p
`^k` (1-p)
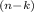`^{(n-k)`, where 'p' is the probability of winning (now 0.5) and 'n choose k' is the binomial coefficient.

To find the probability of winning exactly twice (k=2), we use:

P(X=2) = (3 choose 2) × (0.5)² × 0.5)⁽³⁻²⁾ = 3 × 0.25 × 0.5 = 0.375.

To find the probability of winning all three times (k=3), we use:

P(X=3) = (3 choose 3) × (0.5)³ × (0.5)⁽³⁻³⁾= 1 × 0.125 × 1 = 0.125.

Therefore, the combined probability of winning at least twice is P(X=2) + P(X=3) = 0.375 + 0.125 = 0.5.

Answer 2

Answer: 1/5

Step-by-step explanation:

given data;

chances of winning = 1/3

chances of losing = 1/3

chances of tying in a given round = 1/3

solution:

probability that you would win atleast 2 in any 3 matches without a tied match is

1/3 / ( 2 - 1/3 )

= 1/3 / 5/3

= 1/5

the probability of winning 2 of 3 games without a tie is 1/5