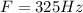Question

Tuning a guitar string, you play a pure 330 Hz note using a tuning device, and pluck the string. The combined notes produce a beat frequency of 5 Hz. You then play a pure 350 Hz note and pluck the string, finding a beat frequency of 25 Hz. What is the frequency of the string note?

Answer 1

The frequency is
`F = 325 Hz`

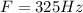
Step-by-step explanation:

From the question we are told that

The frequency for the first note is
`F_1 = 330 Hz`

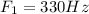
The beat frequency of the first note is
`f_b = 5 \ Hz`

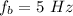
The frequency for the second note is
`F_2 = 350 \ H_z`

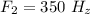
The beat frequency of the first note is
`f_a = 25 \ Hz`

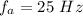
Generally beat frequency is mathematically represented as

`F_(beat) = | F_a - F_b |`

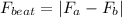
Where
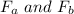`F_a \ and \ F_b` are frequencies of two sound source

Now in the case of this question

For the first note

`f_b = F_1 - F \ \ \ \ \ ...(1)`

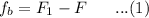
Where F is the frequency of the string note

For the second note

`f_a = F_2 - F \ \ \ \ \ ...(2)`

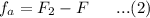
Adding equation 1 from 2

`f_b + f_a = F_1 + F_2 + ( - F) + (-F) )`

`f_b + f_a = F_1 + F_2 -2F`

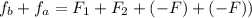
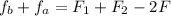
substituting values

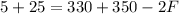
`5 +25 = 330 + 350 -2F`

=>
`F = 325 Hz`