Question

What is the surface area of the prism?

Answer 1

Question 3: 582 ft²

Question 4: 348 in²

Explanation:

Question 3:

Consider the solid shape given as being consisting of two rectangular prism. With careful examination, you'd observe that the offer one beneath has dimensions,
`l, w, h, as 15, 4, 9`

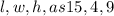
The second one has
`l, w, h, as 6, 4, 6`

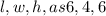
Surface area of the bigger rectangular prism = total surface area - area of the surface that is joined to the smaller rectangular prism.

Area of the face joined to the smaller rectangular prism = 4*6 = 24 ft²

Surface area of the bigger rectangular prism =
`2(wl + hl + hw) - 24`

`2(4*15 + 9*15 + 9*4) - 24`

`462 - 24`

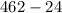
Surface area of the bigger rectangular prism = 438 ft²

Surface area of the smaller rectangular prism = total surface area of rectangular prism - area of the surface that is joined to the bigger rectangular prism.

=
`2(wl + hl + hw) - 24`

`= 2(4*6 + 6*6 + 6*4) - 24`

`= 168 - 24 = 144 ft^2`

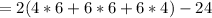
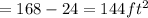
Surface area of the solid = 438 + 144 = 582 ft²

Question 4:

Surface area of the triangular prism is given as: 2(B.A) + P*L

Where,

B.A = area of 1 triangular base = ½*height of the triangle*base of the traingle

B.A = ½*6*16 = 3*16 = 48 in²

P = perimeter of 1 triangular base = sum of all sides of the triangle.

P = 16+10+10 = 36 in

L = length or height of prism =

Plug in the values to find surface area of the prism

Surface area = 2(B.A) + P*L

= 2(48) + 36*7 = 96 + 252 = 348 in²

Surface area of prism = 348 in²