Question

After the solution reaches equilibrium, what concentration of Ni2+(aq) remains? The value of Kf for Ni(NH3)62+ is 2.0×108. Express the concentration to two significant figures and include the appropriate units.

Answer 1

`\large \boxed{1.77 * 10^(-5)\text{ mol/L}}`

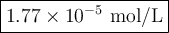
Step-by-step explanation:

Assume that you have mixed 135 mL of 0.0147 mol·L⁻¹ NiCl₂ with 190 mL of 0.250 mol·L⁻¹ NH₃.

1. Moles of Ni²⁺

`n = \text{135 mL} * \frac{\text{0.0147 mmol}}{\text{1 mL}} = \text{1.984 mmol}`

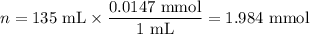
2. Moles of NH₃

`n = \text{190 mL} * \frac{\text{0.250 mmol}}{\text{1 mL}} = \text{47.50 mmol}`

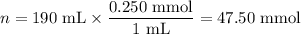
3. Initial concentrations after mixing

(a) Total volume

V = 135 mL + 190 mL = 325 mL

(b) [Ni²⁺]

`c = \frac{\text{1.984 mmol}}{\text{325 mL}} = 6.106 * 10^(-3)\text{ mol/L}`

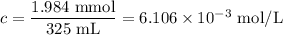
(c) [NH₃]

`c = \frac{\text{47.50 mmol}}{\text{325 mL}} = \text{0.1462 mol/L}`

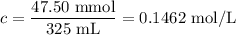
3. Equilibrium concentration of Ni²⁺

The reaction will reach the same equilibrium whether it approaches from the right or left.

Assume the reaction goes to completion.

Ni²⁺ + 6NH₃ ⇌ Ni(NH₃)₆²⁺

I/mol·L⁻¹: 6.106×10⁻³ 0.1462 0

C/mol·L⁻¹: -6.106×10⁻³ 0.1462-6×6.106×10⁻³ 0

E/mol·L⁻¹: 0 0.1095 6.106×10⁻³

Then we approach equilibrium from the right.

Ni²⁺ + 6NH₃ ⇌ Ni(NH₃)₆²⁺

I/mol·L⁻¹: 0 0.1095 6.106×10⁻³

C/mol·L⁻¹: +x +6x -x

E/mol·L⁻¹: x 0.1095+6x 6.106×10⁻³-x

`K_{\text{f}} = \frac{\text{[Ni(NH$_(3)$)$_(6)^(2+)$]}}{\text{[Ni$^(2+)$]}\text{[NH$_(3)$]}^(6)} = 2.0 * 10^(8)`

Kf is large, so x ≪ 6.106×10⁻³. Then

`K_{\text{f}} = \frac{\text{[Ni(NH$_(3)$)$_(6)^(2+)$]}}{\text{[Ni$^(2+)$]}\text{[NH$_(3)$]}^(6)} = 2.0 * 10^(8)\\\\(6.106 * 10^(-3))/(x* 0.1095^(6)) = 2.0 * 10^(8)\\\\6.106 * 10^(-3) = 2.0 * 10^(8)* 0.1095^(6)x= 345.1x\\x= (6.106 * 10^(-3))/(345.1) = 1.77 * 10^(-5)\\\\\text{The concentration of Ni$^(2+)$ at equilibrium is $\large \boxed{\mathbf{1.77 * 10^(-5)}\textbf{ mol/L}}$}`