Question

Given the wavelength of the corresponding emission line, calculate the equivalent radiated energy from n = 4 to n = 2 in both joules and electron volts. Also, calculate the frequency of the wave. λ (Á) = 4861, ƒ(Hz), E(J), E(eV)

Answer 1

f(Hz) = 6.17 × 10¹⁴

E(J) = 4.09 × 10⁻¹⁹

E(ev) = 2.56

Answer 2

Step-by-step explanation:

It is given that,

Initial orbit of electrons,
`n_i=4`

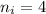
Final orbit of electrons,
`n_f=2`

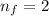
We need to find energy, wavelength and frequency of the wave.

When atom make transition from one orbit to another, the energy of wave is given by :

`E=-13.6((1)/(n_f^2)-(1)/(n_i^2))`

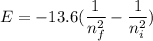
Putting all the values we get :

`E=-13.6((1)/((4)^2)-(1)/((2)^2))\\\\E=2.55\ eV`

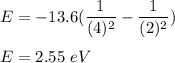
We know that :
`1\ eV=1.6* 10^(-19)\ J`

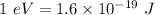
So,

`E=2.55* 1.6* 10^(-19)\\\\E=4.08* 10^(-19)\ J`

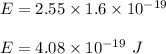
Energy of wave in terms of frequency is given by :

`E=hf`

`f=(E)/(h)\\\\f=(4.08* 10^(-19))/(6.63* 10^(-34))\\\\f=6.14* 10^(14)\ Hz`

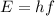
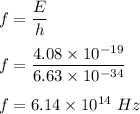
Also,
`c=f\lambda`

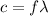
`\lambda` is wavelength

So,

`\lambda=(c)/(f)\\\\\lambda=(3* 10^8)/(6.14* 10^(14))\\\\\lambda=4.88* 10^(-7)\ m\\\\\lambda=488\ nm`

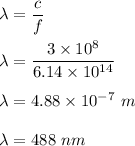
Hence, this is the required solution.