Question

Suppose babies born in a large hospital have a mean weight of 3366 grams, and a variance of 244,036. 1118 babies are sampled at random from the hospital what is the probability that the mean weight of the sample babies would be greater than 3412 gram answer to four decimal places Round your

Answer 1

Answer: 0.0009

Explanation:

Given : Babies born in a large hospital have a mean weight of 3366 grams, and a variance of 244,036.

i.e.
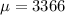`\mu=3366` and
`\sigma^2 = 244036\Rightarrow\ \sigma= √(244036)=494`

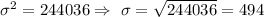
Sample size = 1118

Let
`\overline{X}` be the sample mean weight of babies.

Then, the probability that the mean weight of the sample babies would be greater than 3412 gram:

`P(\overline{X}>3412)=P(\frac{\overline{X}-\mu}{(\sigma)/(√(n))}>(3412-3366)/((494)/(√(1118))))\\\\=P(Z>(46)/(14.7743))\ \ [Z=\frac{\overline{X}-\mu}{(\sigma)/(√(n))}]\\\\\approxP(Z>3.11)\\\\= 1-P(Z<3.11)\\\\=1-0.9991=0.0009`

Hence, the required probability = 0.0009