Question

11. A certain brand of margarine was analyzed to determine the level of polyunsaturated fatty acid (in percent). A sample of 6 packages had an average of 16.98 and sample standard deviation of 0.31. Assuming normality, a 99% confidence interval for the true mean of fatty acid level is:

Answer 1

Answer: (16.47, 17.49)

Explanation:

Formula for confidence interval for the true mean if population stanmdard deviation is unknown:

`\overline{x}\pm t_(\alpha/2)(s)/(√(n))`

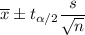
, where
`\overline{x}` = sample mean

n= sample size

s= sample standard deviation

`t_(\alpha/2)` = Two tailed critical value.

We assume that the level of polyunsaturated fatty acid is normally distributed.

Given,

n= 6

degree of freedom = n-1 =5

`\overline{x}` = 16.98

s= 0.31

significance level
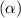`(\alpha)` =1-0.99=0.01

Two tailed t- value for degree of freedom of 5 and significance level of 0.01 =
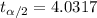`t_(\alpha/2)=4.0317` [by student's t-table]

Now , the 99% confidence interval for the true mean of fatty acid level is:

`16.98\pm 4.0317((0.31)/(√(6)))\\\\=16.98\pm 4.0317(0.126557)\\\\=16.98\pm 0.51024\\\\=(16.98-0.51023,\ 16.98+0.51023)\\\\=(16.46977,\ 17.49023)\approx (16.47,\ 17.49)`

Hence, a 99% confidence interval for the true mean of fatty acid level is: (16.47, 17.49)