Answer:
second option
Explanation:
Given
f(x) = -
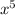 + 9
+ 9
 - 18x³
- 18x³
To find the zeros let f(x) = 0, that is
-
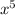 + 9
+ 9
 - 18x³ = 0 ( multiply through by - 1 )
- 18x³ = 0 ( multiply through by - 1 )
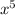 - 9
- 9
 + 18x³ = 0 ← factor out x³ from each term
+ 18x³ = 0 ← factor out x³ from each term
x³ (x² - 9x + 18) = 0 ← in standard form
x³(x - 3)(x - 6) = 0 ← in factored form
Equate each factor to zero and solve for x
x³ = 0 ⇒ x = 0 with multiplicity 3
x - 3 = 0 ⇒ x = 3 with multiplicity 1
x - 6 = 0 ⇒ x = 6 with multiplicity 1