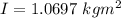Answer:
The moment of inertia is
Step-by-step explanation:
From the question we are told that
The frequency is

The mass of the pendulum is
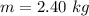
The location of the pivot from the center is
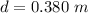
Generally the period of the simple harmonic motion is mathematically represented as
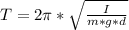
Where I is the moment of inertia about the pivot point , so making I the subject of the formula it
=>
![I = [ (T)/(2 \pi ) ]^2 * m* g * d](https://img.qammunity.org/2021/formulas/physics/college/2mh7319c7owxbyduq5zcifm954x4zhv55g.png)
But the period of this simple harmonic motion can also be represented mathematically as
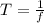
substituting values
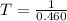
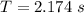
So
![I = [ (2.174)/(2 * 3.142 ) ]^2 * 2.40* 9.8 * 0.380](https://img.qammunity.org/2021/formulas/physics/college/h6wnqqxnomxqjdgwqky8cfxz40nxe2f6h1.png)