Answer:
0.65463
Explanation:
From the given question:
It is stated that 2% of the parts are defective (D) out of 50 parts
Therefore the probability of the defectives;
i.e p(defectives) =
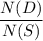
p(defectives) =
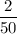
p(defectives) = 0.04
The probability of the failure is the P(Non-defectives)
p(Non-defectives) = 1 - P(defectives)
p(Non-defectives) = 1 - 0.04
p(Non-defectives) = 0.96
Also , Let Y be the number of non -defective out of the 52 stock parts.
and we need Y ≥ 50
P( Y ≥ 50) , n = 52 , p = 0.96
P( Y ≥ 50) = P(50 ≤ Y ≤ 52) = P(Y = 50, 51, 52)
= P(Y = 50) + P(Y =51) + P(Y=52) (disjoint events)
P(Y = 50) =
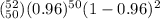
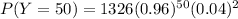
P(Y = 50) = 0.27557
P(Y = 51) =
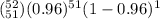
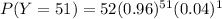
P(Y = 51) = 0.25936
(Y = 52) =
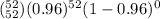

P(Y = 52) = 0.1197
∴
P(Y = 50) + P(Y =51) + P(Y=52) = 0.27557 + 0.25936 + 0.1197
P(Y = 50) + P(Y =51) + P(Y=52) = 0.65463