Question

1

If the 2nd and 5th terms of a G.P are 6 and 48 respectively, find the sum of the first for term

Answer 1

If the first term is
`a`, then the second term is
`ar`, the third is
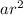`ar^2`, the fourth is
`ar^3`, and the fifth is
`ar^4`.

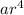We're given

`\begin{cases}ar=6\\ar^4=48\end{cases}\implies(ar^4)/(ar)=r^3=8\implies r=2\implies a=3`

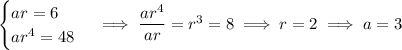
So the first five terms in the GP are

3, 6, 12, 24, 48

Adding up the first four gives a sum of 45.

If you were asked to find the sum of many, many more terms, having a formula for the n-th partial sum would convenient. Let
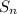`S_n` denote the sum of the first n terms in the GP:

`S_n=3+3\cdot2+3\cdot2^2+\cdots+3\cdot2^(n-2)+3\cdot2^(n-1)`

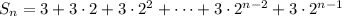
Multiply both sides by 2:

`2S_n=3\cdot2+3\cdot2^2+3\cdot2^3+\cdots+3\cdot2^(n-1)+3\cdot2^n`

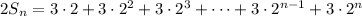
Subtract this from
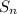`S_n`, which eliminates all the middle terms:

`S_n-2S_n=3-3\cdot2^n\implies -S_n=3(1-2^n)\implies S_n=3(2^n-1)`

Then the sum of the first four terms is again
`S_4=3(2^4-1)=45`.