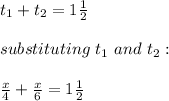Question

Juan jogs each day from his house to a local park, and then he jogs back along the same route. On his way to the park, he averages 4 miles per hour. On his way home, he averages 6 miles per hour. If the total trip takes 1 and one-half hours, which equation can be used to find x, the distance in miles from Juan's house to the park? Distance (mi) Rate (mi/hr) Time (hr) Trip to Park x 4 mph Trip to Home x 6 mph StartFraction x Over 4 EndFraction + StartFraction x Over 6 EndFraction = 1 StartFraction x Over 4 EndFraction + StartFraction x Over 6 EndFraction = 1 and one-half 4 x + 6 x = 1 and one-half 4 x + 6 x = 1

Answer 1

B

Explanation:

Edg. 2020

Answer 2

`(x)/(4)+ (x)/(6)=1(1)/(2)`

Explanation:

Speed is the ratio of distance traveled to the total time taken. It is given by the equation:

speed = distance / time.

Given that the distance to the park = x miles.

On his way to the park, he averages 4 miles per hour. Let the time taken be
`t_1` therefore:

speed = distance / time.

4 = x /
`t_1`

`t_1` = x / 4

On his way home, he averages 6 miles per hour Let the time taken be
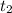`t_2` therefore:

speed = distance / time.

6 = x /
`t_2`

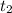
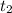`t_2` = x / 6

The total trip takes 1 and one-half hours, therefore:

`t_1+t_2=1(1)/(2)\\\\ substituting\ t_1 \ and\ t_2:\\\\(x)/(4)+ (x)/(6)=1(1)/(2)`