Question

2) A basketball player scores 70% of his shots on average. What is the probability that he scores at least 18 successful shots tonight if he gets 20 shots?

Answer 1

3.54%

Explanation:

This question represents a binomial distribution. A binomial distribution is given by:

`P(x)=(n!)/((n-x)!x!) p^xq^(n-x)`

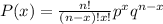
Where n is the total number of trials, p is the probability of success, q is the probability of failure and x is the number of success.

Given that:

A basketball player scores 70% of his shots on average, therefore p = 70% = 0.7. Also q = 1 - p = 1 - 0.7 = 0.3.

The total number of trials (n) = 20 shots

The probability that he scores at least 18 successful shots tonight if he gets 20 shots = P(x = 18) + P(x = 19) + P(x = 20)

P(x = 18) =
`(20!)/((20-18)!18!)*0.7^(18)*0.3^(20-18)=0.0278`

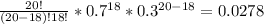
P(x = 19) =
`(20!)/((20-19)!19!)*0.7^(19)*0.3^(20-19)=0.0068`

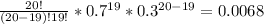
P(x = 20) =
`(20!)/((20-20)!20!)*0.7^(20)*0.3^(20-20)=0.0008`

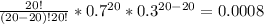
The probability that he scores at least 18 successful shots tonight if he gets 20 shots = P(x = 18) + P(x = 19) + P(x = 20) = 0.0278 + 0.0068 + 0.0008 = 0.0354 = 3.54%