Question

Kelly is a waitress and her average tip rate is 18%. After taking a sample of her tips from a week, she thinks her tip rate is actually higher. The data below is the tip rate for 15 randomly chosen checks (the numbers represent percentage). Assume that tip rates are normally distributed.

18.5 18.2 20 21.3 17.9 17.9 18.1 17.5 20 18
a) Express the null and alternative hypotheses in symbolic form for this claim.
H0 : Select an answer
Ha: Select an answer
b) What is the test statistic. Round to 2 decimals.
c) What is the p-value. Round to 4 decimals p-value =

Answer 1

Explanation:

From the given information:

the null and alternative hypotheses in symbolic form for this claim can be computed as:

`H_o:\mu = 18 \\ \\ H_a : \mu > 18`

Mean =
`(18.5+18.2+20+21.3+17.9+17.9+18.1+17.5+20+18)/(10)`

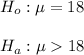
Mean = 18.74

Standard deviation
`\sigma = \sqrt{(\sum(x_i - \mu)^2)/(N)}`

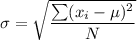
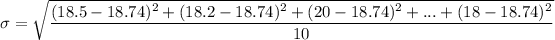
Standard deviation
`\sigma = \sqrt{((18.5 - 18.74)^2+(18.2 - 18.74)^2+(20 - 18.74)^2+...+(18 - 18.74)^2)/(10)}`

Standard deviation
`\sigma` = 1.18

The test statistics can be computed as follows:

`Z= (X- \mu)/((\sigma)/(√(n)))`

`Z= (18.6- 18)/((1.18)/(√(10)))`

`Z= (0.6)/((1.18)/(3.162))`

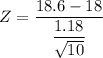
Z = 1.6078

Z = 1.61

Degree of freedom = n -1

Degree of freedom = 10 -1

Degree of freedom = 9

Using t - calculator at Z = 1.6078 and df = 9

The P - value = 0.0712