Answer:
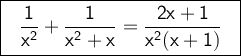
Explanation:
Hello,
This is the same method as computing for instance:
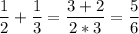
We need to find the same denominator.
Let's do it !
For any x real different from 0, we can write:
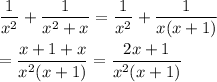
Hope this helps.
Do not hesitate if you need further explanation.
Thank you