Answer:
64 in²
Explanation:
Given that the two figures are similar, therefore, the ratio of the area areas of both figures is proportional to the ratio of the square of the corresponding side lengths of both figures. This means:
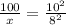
Where x is the area of the other figure.
Solve for x
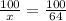
Cross multiply
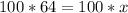
Divide both sides by 100
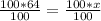
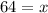
Area of the other figure = 64 in²