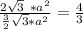Question

Find the area ratio of a regular octahedron and a tetrahedron regular, knowing that the diagonal of the octahedron is equal to height of the tetrahedron.

Answer 1

`(4)/(3)`

Explanation:

The area of a regular octahedron is given by:

area =
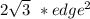`2√(3)\ *edge^2`. Let a is the length of the edge (diagonal).

area =
`2√(3)\ *a^2`

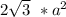
Given that the diagonal of the octahedron is equal to height (h) of the tetrahedron i.e.

a = h, where h is the height of the tetrahedron and a is the diagonal of the octahedron. Let the edge of the tetrrahedron be e. To find the edge of the tetrahedron, we use:

`h=\sqrt{(2)/(3) } e\\but\ h=a\\a=\sqrt{(2)/(3) } e\\e=\sqrt{(3)/(2) }a`

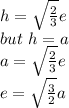
The area of a tetrahedron is given by:

area =
`√(3)\ *edge^2` =
`√(3) *(\sqrt{(3)/(2) }a)^2=(3)/(2)√(3) *a^2`

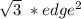The ratio of area of regular octahedron to area tetrahedron regular is given as:

Ratio =
`(2√(3)\ *a^2)/((3)/(2) √(3)*a^2) =(4)/(3)`