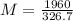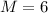Answer:
a

b
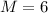
Step-by-step explanation:
From the question we are told that
The mass of the rock is
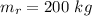
The length of the small object from the rock is
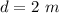
The length of the small object from the branch
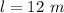
An image representing this lever set-up is shown on the first uploaded image
Here the small object acts as a fulcrum
The force exerted by the weight of the rock is mathematically evaluated as
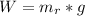
substituting values
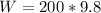

So at equilibrium the sum of the moment about the fulcrum is mathematically represented as
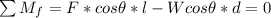
Here
 is very small so
is very small so

and
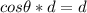
Hence
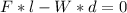
=>
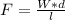
substituting values
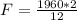

The mechanical advantage is mathematically evaluated as
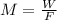
substituting values