Question

UA Hamburger Hamlet (UAHH) places a daily order for its high-volume items (hamburger patties, buns, milk, and so on). UAHH counts its current inventory on hand once per day and phones in its order for delivery 24 hours later. Determine the number of hamburgers UAHH should order for the following conditions:

Average daily demand 600
Standard deviation of demand 100
Desired service probability 99%
Hamburger inventory 800

Answer 1

730 items

Step-by-step explanation:

The objective of the given information is to determine the number of hamburgers UAHH should order for the following conditions:

Average daily demand 600

Standard deviation of demand 100

Desired service probability 99%

Hamburger inventory 800

The formula for a given order quantity in a fixed period of time can be expressed as :

`q = \overline d(L+T)+ z \sigma_(L+T)-I`

where;

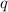`q` = order quantity = ???

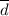`\overline d` = daily demand average = 600

L = lead time in days = 1

T = time taken = 1

z = no of standard deviation = ???

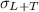`\sigma_(L+T)` = standard deviation of usage in lead time and time taken = ???

I = present inventory level = 800

`\sigma_(L+T)` =
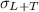`\sqrt 2` × standard deviation of daily demand

`\sigma_(L+T)` =
`√(2) *100`

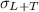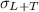`\sigma_(L+T)` = 1.4142 * 100

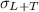`\sigma_(L+T)` = 141.42 items

From the Desired service probability 99% = 0.99; we can deduce the no of standard deviation by using the excel function (=NORMSINV (0.99))

z = 2.33

From
`q = \overline d(L+T)+ z \sigma_(L+T)-I`

`q =600(1+1)+ 2.33*(141.42)-800`

`q =600(2)+ 2.33*(141.42)-800`

`q =1200+329.5086-800`

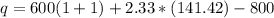
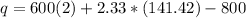
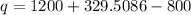
q = 729.5086 items

q ≅ 730 items

Therefore; the number of hamburgers UAHH should order from the following given conditions = 730 items