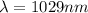Answer:
The wavelength is
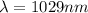
Step-by-step explanation:
From the question we are told that
The wavelength of the left light is
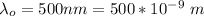
The voltage across A and B is
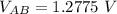
Let the stopping potential at A be
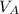 and the electric potential at B be
and the electric potential at B be
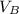
The voltage across A and B is mathematically represented as
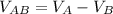
Now According to Einstein's photoelectric equation the stopping potential at A for the ejected electron from the left side in terms of electron volt is mathematically represented as
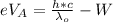
Where W is the work function of the metal
h is the Planck constant with values
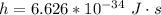
c is the speed of light with value
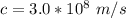
And the stopping potential at B for the ejected electron from the right side in terms of electron volt is mathematically represented as
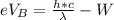
So
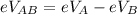
=>
![eV_(AB) = (h * c)/(\lambda_o ) - W - [(h * c)/(\lambda ) - W]](https://img.qammunity.org/2021/formulas/physics/college/g91ypgfe6ie14lkh59cs5qqjnkbtm03k5w.png)
=>
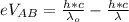
=>
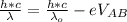
=>

Where e is the charge on an electron with the value

=>
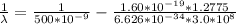
=>

=>

=>