Question

How do the areas of triangle ABC and DEF compare? The area of △ABC is 1 square unit less than the area of △DEF. The area of △ABC is equal to the area of △DEF. The area of △ABC is 1 square unit greater than the area of △DEF. The area of △ABC is 2 square units greater than the area of △DEF.

Answer 1

b

Explanation:

edge exam

Answer 2

The area of △ABC is equal to the area of △DEF

Explanation:

On a coordinate plane, triangles A B C and D E F are shown. Triangle A B C has points (4, 2), (7, 2), (4, 6). Triangle D E F has points (negative 2, negative 1), (4, negative 3), and (4, negative 1).

How do the areas of triangle ABC and DEF compare? The area of △ABC is 1 square unit less than the area of △DEF. The area of △ABC is equal to the area of △DEF. The area of △ABC is 1 square unit greater than the area of △DEF. The area of △ABC is 2 square units greater than the area of △DEF.

Answer: The length of the sides of the triangle ABC are given below:

`AB=√((7-4)^2+(2-2)^2) =3\ unit\\\\BC=√((4-7)^2+(6-2)^2) =5\ unit\\\\AC=√((4-4)^2+(6-2)^2) =4\ unit`

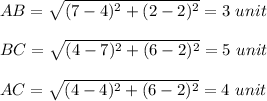
The area of triangle ABC is given as:

Area = 1/2 × base × height = 1/2 × 3 × 4 = 6 unit²

The length of the sides of the triangle DEF are given below:

`DE=√((4-(-2))^2+(-3-(-1))^2) =√(40) \ unit\\\\EF=√((4-2)^2+(-1-(-3))^2) =2 \ unit\\\\DF=√((4-(-2))^2+(-1-(-1))^2) =6 \ unit`

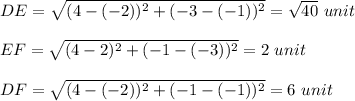
The area of triangle DEF is given as:

Area = 1/2 × base × height = 1/2 × 2 × 6 = 6 unit²

The area of triangle ABC is equal to 6 unit² and the area of triangle DEF is equal to 6 unit² , therefore The area of △ABC is equal to the area of △DEF