Question

Suppose a poll of 700 voters says that 45% of the voters will vote for Candidate A for president. Compute the 99% confidence interval

Answer 1

Answer: (0.4016, 0.4984).

Explanation:

Let p be the proportion of voters will vote for Candidate A for president.

Formula for confidence interval for proportion:

`\hat{p}\pm z^*\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}`

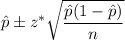
, here
`\hat{p}`= sample proportion

n= sample size.

z* =two-tailed critical z- value.

As per given, we have

n= 700

`\hat{p}` = 0.45

Critical two-tailed z-value for 99% confidence interval = 2.576

Then, the required 99% confidence interval for p would be:

`0.45\pm (2.576)\sqrt{(0.45(1-0.45))/(700)}\\\\=0.45\pm(2.576)√(0.000353571428)\\\\=0.45\pm (2.576)(0.0188035)\\\\=0.45\pm0.04844\\\\=(0.45-0.048437,\ 0.45+0.048437)\\\\=(0.401563,\ 0.498437)\approx(0.4016,\ 0.4984)`

Hence, the required confidence interval (0.4016, 0.4984).