Answer:
The correct answer is 25.2 in.
Explanation:
It is given that number line goes from 0 to 60 which can be used to represent a ribbon of length = 60 inches.
2 inches of the ribbon are frayed so actual length = 58 inches
Please refer to the attached image for the ribbon.
A is at 0
C is at 60
B is at 2
P is the point to divide the remaining ribbon in the ratio 2:3.
Part AB of the ribbon is frayed.
BP: PC = 2:3
Let BP = 2
 and PC = 3
and PC = 3

Now, BP + PC = BC = 58 = 2
 + 3
+ 3
 = 5
= 5

So,
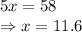
BP =
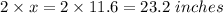
Location of the Cut = 2 + 23.2 = 25.2 inches
Alternatively, we can use the formula directly:
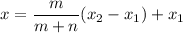
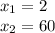
m: n is the ratio 2:3
