Answer:
The expected value of the game is $0.33.
Explanation:
There are N = 36 outcomes of rolling two 6-sided fair dice.
The sample for the sum of two numbers to be 7 is:
S = {(1, 6), (2, 5), (3, 4), (4, 3), (5, 2) and (6, 1)}
n (S) = 6
It is provided that there is a 7 to 1 odds against rolling a sum of 6 with the roll of two fair dice.
That is, you win $7 if you succeed and you lose $1 if you fail.
Compute the expected value of the game as follows:
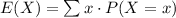
![=[\$(7)* (6)/(36)]+[\$(-1)* (30)/(36)]\\\\=(7)/(6)-(5)/(6)\\\\=(7-5)/(6)\\\\=(1)/(3)\\\\=\$0.33](https://img.qammunity.org/2021/formulas/mathematics/college/fljfc35ttpm1nmm43oqxhymklkbqibdfbd.png)
Thus, the expected value of the game is $0.33.