Question

Which function has a domain where x does not =3 and a range where y does not =2? A. f(x)=(x-5)/(x+3) B. f(x)=2(x+5)/(x+3) C. 2(x+5)/(x-3) D. (x+5)/(x-3)

Answer 1

OPTION D IS NOT CORRECT.

i took the test & selected D and it was wrong.

THE CORRECT ANSWER IS C.

Explanation:

Answer 2

Answer: D. (x+5)/(x-3)

Explanation:

Domain = Set of all input values of a function.

range = set of all output values of a function.

Given: Domain:
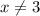`x\\eq3` ; range =
`y\\eq2`

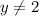
We do not include a value for domain if it makes the expression indeterminant .

Since all the functions in options are fractions, here the denominator does not equal to 0.

But in option C and D, the denominator can be zero if x=3.

So , domain for then it
`x\in {R-3}`

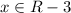
Also, for option C if
`2=2((x+5))/((x-3))`

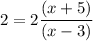
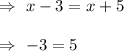`\Rightarrow\ x-3=x+5\\\\\Rightarrow\ -3=5`.which is not true.

Wher as in option D,
`2=(x+5)/(x-3)\Rightarrow\ 2x-6=x+5\Rightarrow\ x=11`

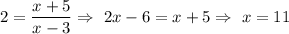
Hence, Domain:
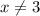`x\\eq3` ; range =
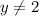`y\\eq2` is for option D.