Answer:
A. The series CONVERGES
Explanation:
If
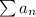 is a series, for the series to converge/diverge according to ratio test, the following conditions must be met.
is a series, for the series to converge/diverge according to ratio test, the following conditions must be met.

If
 < 1, the series converges absolutely
< 1, the series converges absolutely
If
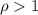 , the series diverges
, the series diverges
If
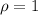 , the test fails.
, the test fails.
Given the series
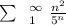
To test for convergence or divergence using ratio test, we will use the condition above.
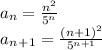
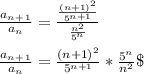
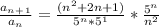
aₙ₊₁/aₙ =
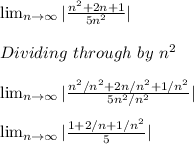
note that any constant dividing infinity is equal to zero
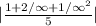
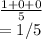
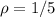
Since The limit of the sequence given is less than 1, hence the series converges.