Answer:
Explanation:
Given that:
Sample size n = 11
Sample Mean X = 26500
standard deviation = 6000
Population mean
 = 31000
= 31000
the null and alternate hypotheses are being stated as follows:
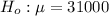
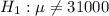
The value of the test statistic can be computed as:
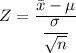
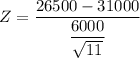
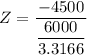
Z = −2.4875
Z = −2.49
The degree of freedom df = n- 1
The degree of freedom df = 11 - 1
The degree of freedom df = 10
At the level of significance ∝ = 0.05
 = 0.025
= 0.025
From the t distribution table at
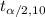 and critical value = -2.49;
and critical value = -2.49;
The p-value = 0.0320
Decision Rule: Reject null hypothesis if p -value is lesser than the level of significance
Conclusion:We reject the null hypothesis , therefore, we conclude that there is no sufficient information to that the mean tuition and fees for private colleges is different from $31,000