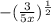Answer:
a.
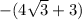
b.
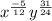
c.
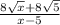
d.
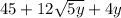
e.
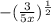
Explanation:
a.
![√(12) - √(108) - \sqrt[3]{27}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/avn32m7555odrpkxbhqqwrzkqrvgexc4ar.png)
Expand each expression
![√(4*3) - √(36 * 3) - \sqrt[3]{3*3*3}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/mq8nv9nyebipr2ss5pys895g4ylhxwxhf3.png)
Split the first two surds
![√(4)*√(3) - √(36) * √(3) - \sqrt[3]{3*3*3}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/n7oy1ehx82b2mmuoh857z7hv7ncoopd4go.png)
![2*√(3) - 6 * √(3) - \sqrt[3]{3*3*3}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/7uue7ztv285yi5po10ksd03jtr96v9kixn.png)
Apply law of indices
![2*√(3) - 6 * √(3) - \sqrt[3]{3^3}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/kad8qn2htquxun2iwpn2nfv5fjeayq56cz.png)
Apply law of indices
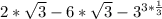
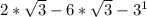
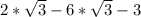
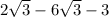
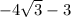
Factorize
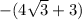
The expression cannot be further simplified
b.
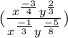
Expand the expression
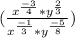
Apply the following law of indices;
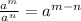
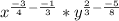
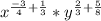
Add the exponents
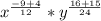
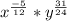
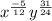
The expression cannot be further simplified
c.
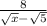
Rationalize the denominator
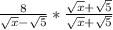
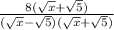
Simplify the numerator
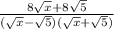
Simplify the denominator by difference of two squares
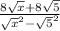
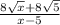
The expression cannot be further simplified
d.
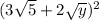
Expand the expression
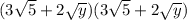
Open the bracket
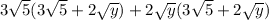
Open both brackets
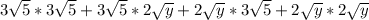
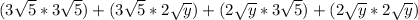
Multiply each expression in the bracket
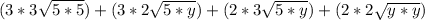
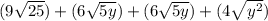
Solve like terms
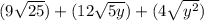
Take square root of 25 and y²
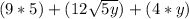
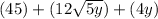
Remove the brackets
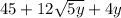
The expression cannot be further simplified
e.
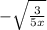
This expression can not be simplified; However, it can be rewritten, by applying law of indices as