Question

Astronomers have recently observed stars orbiting at very high speeds around an unknown object near the center of our galaxy. For stars orbiting at distances of about 1014 m from the object, the orbital velocities are about 106 m/s. Assume the orbits are circular, and estimate the mass of the object, in units of the mass of the sun (MSun = 2x1030 kg). If the object was a tightly packed cluster of normal stars, it should be a very bright source of light. Since no visible light is detected coming from it, it is instead believed to be a supermassive black hole.

Answer 1

The mass of the object is 745000 units of the sun

Step-by-step explanation:

We know that the centripetal force with which the stars orbit the object is represented as

`F_(c)` =
`(mv^(2) )/(r)`

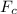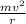
and this centripetal force is also proportional to

`F_(c)` =
`(kMm)/(r^(2) )`

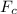where

m is the mass of the stars

M is the mass of the object

v is the velocity of the stars = 10^6 m/s

r is the distance between the stars and the object = 10^14 m

k is the gravitational constant = 6.67 × 10^-11 m^3 kg^-1 s^-2

We can equate the two centripetal force equations to give

`(mv^(2) )/(r)` =
`(kMm)/(r^(2) )`

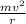which reduces to

`v^(2)` =
`(kM)/(r)`

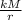
and then finally

M =
`(rv^(2) )/(k)`

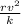
substituting values, we have

M =
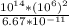`(10^(14)*(10^(6))^(2) )/(6.67*10^(-11) )` = 1.49 x 10^36 kg

If the mass of the sun is 2 x 10^30 kg

then, the mass of the the object in units of the mass of the sun is

==> (1.49 x 10^36)/(2 x 10^30) = 745000 units of sun