Answer:
Explanation:
We are going to use the areas given to find the lengths of the sides of each of their respective squares. For the purple square, the area is 35 units squared. Because the formula for the area is A = s * s, then we can fill in the value for the area and solve for s, the side length, of the purple square.
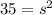 and
and
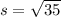 . That side length also serves as the height of the right triangle. Now on to the blue square on the bottom. It has an area of 50 units squared, so
. That side length also serves as the height of the right triangle. Now on to the blue square on the bottom. It has an area of 50 units squared, so
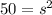 and
and
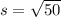 . We could feasibly simplify that, but it's not necessary, really. That side serves as the base of the right triangle. Now we can use Pythagorean's Theorem to find the length of the hypotenuse of the right triangle, which also serves as the side of the big blue square. We will call the side of the big blue square x.
. We could feasibly simplify that, but it's not necessary, really. That side serves as the base of the right triangle. Now we can use Pythagorean's Theorem to find the length of the hypotenuse of the right triangle, which also serves as the side of the big blue square. We will call the side of the big blue square x.
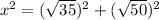 and
and
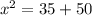 and
and
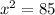 and
and
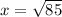 . That is the side length of the large blue square. The area for the square is s * s, and since we know the side length to be √85:
. That is the side length of the large blue square. The area for the square is s * s, and since we know the side length to be √85:
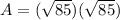 so
so
A = 85 units squared