Question

It is believed that 4​% of children have a gene that may be linked to juvenile diabetes. Researchers at a firm would like to test new monitoring equipment for diabetes. Hoping to have 21 children with the gene for their​ study, the researchers test 733 newborns for the presence of the gene linked to diabetes. What is the probability that they find enough subjects for their​ study?

Answer 1

the probability that they find enough subjects for their​ study is 0.9515

Explanation:

From the given information:

Let X be the random variable that follows a normal distribution.

Therefore:

X
`\sim`Binomial(n=733,p=0.04)

`\mu = np`

`\mu = 733*0.04`

`\mu = 29.32`

`\sigma = √(np(1-p))`

`\sigma = √(29.32(1-0.04))`

`\sigma = √(29.32(0.96))`

`\sigma = √(28.1472)`

`\sigma = 5.305`

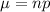
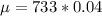
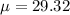
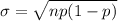
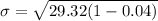
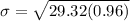
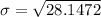
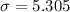
The probability of P(X ≥ 21) lies in the region between 20.5 and 21.5 by considering a discrete contribution of a continuous normal distribution. Eventually, X > 20.5

∴

P(X >20.5)= P(Z > z)

Using standard normal z formula:

`z = (x-\mu)/(\sigma)`

`z = (20.5-29.32)/(5.305)`

`z = (-8.82)/(5.305)`

`z = -1.662582`

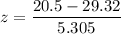
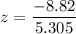
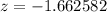
z = -1.66

P(X >20.5)= P(Z > -1.66)

From the standard z tables ;

P(X >20.5)= 1 - 0.0485

P(X >20.5)= 0.9515