Question

Students in management science class have just received their grades on the first test. The instructor has provided information about the first test grades in some previous classes as well as the final average for the same students. Some of these grades have been sampled and are as follow:

1st test Grade 98 77 88 80 96 61 64 95 79
Final average 93 78 84 75 84 64 66 95 86
Develop a regression model that could be used to predict the final average in the course based on the first test grade.
Predict the final average of a students who made an 83 on the first test.
Give the value of r and r2 for this model.
Interpret the value of r2 in the context of this problem.

Answer 1

The regression model is:

y = 20.29 + 0.73·x

Explanation:

In this case a regression model is to be formed to predict the final average in the course based on the first test grade.

Use Excel to form the regression model.

The output is attached below.

The regression model is:

y = 20.29 + 0.73·x

Predict the final average of a students who made an 83 on the first test as follows:

y = 20.29 + 0.73·x

= 20.29 + 0.73 × 83

= 80.88

The final average of a students who made an 83 on the first test would be 80.88.

From the output:

R² = 0.839

Then the correlation coefficient will be:

`r=\sqrt{R^(2)}=√(0.839)=0.91597\approx 0.92`

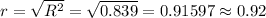
The value of r is 0.92.

The coefficient of determination R² specifies the percentage of the variance in the dependent-variable (Y) that is forecasted or explained by linear regression and the forecaster variable (X, also recognized as the independent-variable).

In this case, the R² value of 0.839 implies that 83.9% of the variation in the final average can be explained by the grades in the first test.