Answer:
11
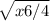
Given:
The triangle on the left ( triangle 1) has a 60º, a 90º, and a side that equals 11.
So we know the triangle on the right (triangle 2) has a 45º and a 90º angle.
Triangle 2
Since triangle angles always have a sum of 180º, we can solve for the third angle of triangle 2. 180 - (45 + 90) = 45. So the third angle of triangle 2 is 45º.
This is a special type of right triangle called a 45-45-90. An image of the leg/hypotenuse is uploaded below. Meaning, if we solve for the leg that joins the two triangles, we can solve for the hypotenuse.
Triangle 1
To solve for the middle leg, we work with the information we have. So first, find the third angle. 190 - (60 + 90) = 30. This brings us to a second type of special right triangle. An image of the leg/hypotenuse is uploaded below.
Given that we have a side angle of 11, we know that is 2x due to orientation. So 2x=11 simplifies to x=5.5. We then plug that back in to find the leg that we want: 5.5
 .
.
Triangle 2
Now that we have a side length for the second triangle we can solve. x for this triangle is 5.5
 so to find the hypotenuse we plug into x
so to find the hypotenuse we plug into x
 . This turns into (5.5
. This turns into (5.5

 ) which simplifies into 5.5
) which simplifies into 5.5
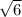 = 13.47
= 13.47
Answers
The answers are not in the correct form. By going through and finding the decimal form of each, you find out that 11
 is equivalent to 13.47, therefore your answer.
is equivalent to 13.47, therefore your answer.