Answer:
1)

2)

3)

4)
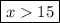
5)

6)

7)

8)

9)

10)

Explanation:
1)

Adding 7 to both sides
=> 2x > 3+7
=> 2x > 10
Dividing both sides by 2
=> x > 5
2)
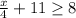
Subtracting 11 to both sides
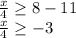
Multiplying both sides by 4
x ≥ -3 * 4
x ≥ -12
3) -6x+7 ≥ 19
Subtracting 19 to both sides
=> -6x ≥ 19-7
=> -6x ≥ 12
Dividing both sides by -6
=> x ≤ -2
4) -10 + 4x > 50
Adding 10 to b.s
=> 4x > 50+10
=> 4x > 60
Dividing b.s by 4
=> x > 15
5)
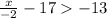
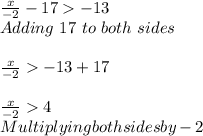
=> x < 4*-2
=> x < -8
6) 8 - 2x ≤ 46
Subtracting 8 from b.s
=> -2x ≤ 46-8
=> -2x ≤ 38
Dividing b.s by -2
=> x ≥ -19
7) -13x+1 ≤ -25
Subtracting 1 from both sides
=> -13x ≤ -25-1
=> -13x ≤ -26
Dividing both sides by -13
=> x ≥ 2
8)
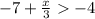
Adding 7 to b.s
=> x/3 > -4+7
=> x/3 > 3
Multiplying 3 to b.s
=> x > 3*3
=> x > 9
9) -9x-19 ≥ 17
Adding 19 to both sides
=> -9x ≥ 17+19
=> -9x ≥ 36
Dividing both sides by -9
=> x ≤ -4
10) 16 - x > 9
Adding x to both sides
=> 16 > 9 + x
Subtracting 9 from both sides
=> 16 - 9 > x
=> 7 > x
OR
=> x < 7
NOTE: Whenever, we divide the inequality by a negative signed term, the inequality changes to its opposite.