Question

To measure a stone face carved on the side of a​ mountain, two sightings 700 feet from the base of the mountain are taken. If the angle of elevation to the bottom of the face is 35degreesand the angle of elevation to the top is 38 degrees​,what is the height of the stone​ face

Answer 1

Height of stone face is : 56.7 ft

Explanation:

Kindly refer to the attached image for the diagram of the given conditions and values.

Let C be the base of mountain.

D be the point from where two sightings are taken.

AB be the stone face.

Angle of elevations:

`\angle BDC =35^\circ\\\angle ADC =38^\circ`

To find:

Height of stone face = ?

AB = ?

Solution:

We can use trigonometric function of tangent here in two triangles
`\triangle BCD\ and\ \triangle ACD`:

`In\ \triangle BCD :`

`tan(\angle BDC) = (Perpendicular)/(Base) = (BC)/(CD)\\\Rightarrow BC = 700 * tan35 ..... (1)`

`In\ \triangle ACD :`

`tan(\angle ADC) = (Perpendicular)/(Base) = (AC)/(CD)\\\Rightarrow AC = 700 * tan38\\\Rightarrow AB +BC = 700 * tan38\\\\\text{Using equation (1):}\\\Rightarrow AB + 700 * tan 35 = 700 * tan 38\\\Rightarrow AB = 700 * tan 38-700 * tan35\\\Rightarrow AB = 700 * (tan 38-tan35)\\\Rightarrow AB = 700 * 0.081\\\Rightarrow AB = \bold{56.7}\ ft`

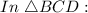
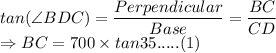
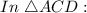
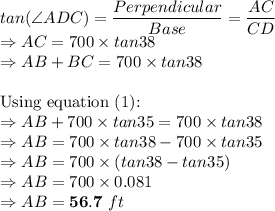
So, Height of stone face is : 56.7 ft