Question

A soup company puts 12 ounces of soup in each can. The company has determined that 97% of cans have the correct amount. Which of the following describes a binomial experiment that would determine the probability that a case of 36 cans has all cans that are properly filled?

a. n=36, p=0.97, x=1
b. n=12, p=0.36, x=97
c. n=12, p=0.97, x=0
d. n=36, p=0.97, x=36

Answer 1

Option d: n = 36, p = 0.97, x = 36.

Explanation:

We are given that a soup company puts 12 ounces of soup in each can. The company has determined that 97% of can have the correct amount.

We have to describe a binomial experiment that would determine the probability that a case of 36 cans has all cans that are properly filled.

Let X = Number of cans that are properly filled

The above situation can be represented through binomial distribution;

`P(X = x) = \binom{n}{x} * p^(x) * (1-p)^(n-x) ; x = 0,1,2,........`

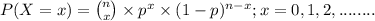
where, n = number of trials (samples) taken = 36 cans

x = number of success = all cans are properly filled = 36

p = probabilitiy of success which in our question is probability that

can have the correct amount, i.e. p = 97%

So, X ~ Binom (n = 36, p = 0.97)

Hence, from the options given the correct option which describes a binomial experiment that would determine the probability that a case of 36 cans has all cans that are properly filled is n = 36, p = 0.97, x = 36.